위상 정렬을 공부하는 와중에 이해가 가지 않는 부분이 있는데,
긴가민가해서 정확히 눈으로 확인해보고 싶어 직접 그림으로 풀어보았다.
이해가 가지 않는 부분은 다음과 같다.
모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있습니다.
-> 사이클에 포함된 원소 중에서 어떠한 원소도 큐에 들어가지 못합니다.
왜 사이클에 포함된 원소는 어떤 것도 큐에 들어가지 못할까? 라는 생각이 들었는데, 머릿속으로 큐에 집어넣었다가 빼면서 하려니 중간에 실수를 할 수도 있을 것 같아서 바로 그림으로 그려보았다.
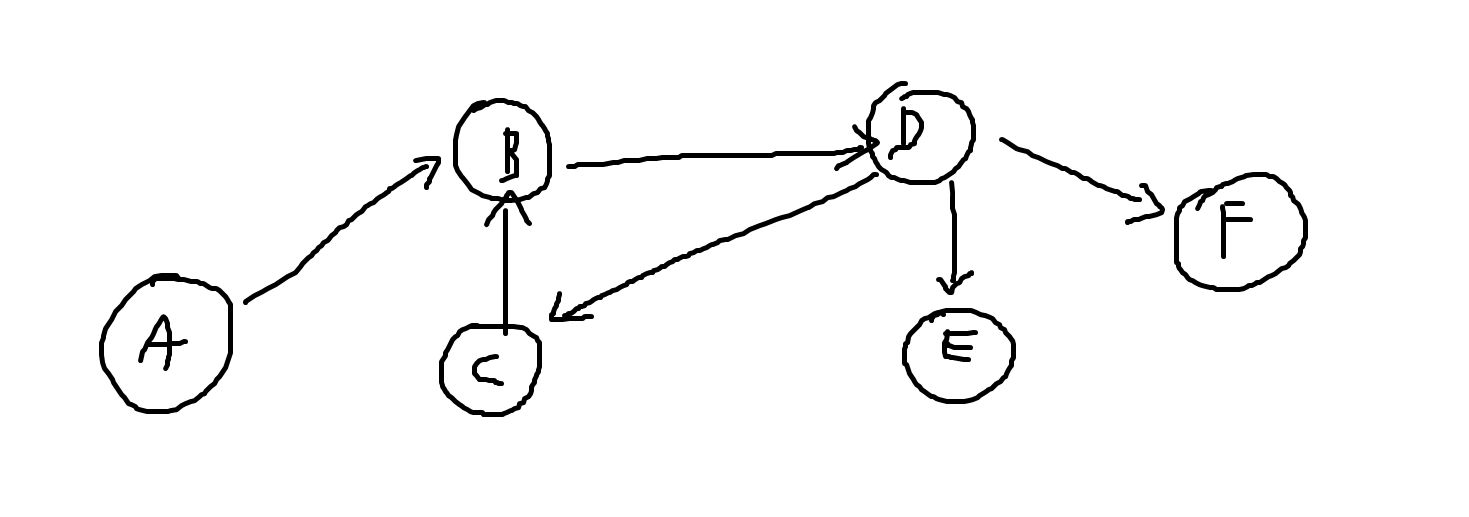
다음과 같이 사전에 준비된 그래프가 존재한다. 그리고 보면 알겠지만 (B -> D -> C -> B) 로의 사이클이 존재한다.
그럼 이제 A를 큐에 집어넣고, 간선을 삭제하면 다음과 같이 진행된다.
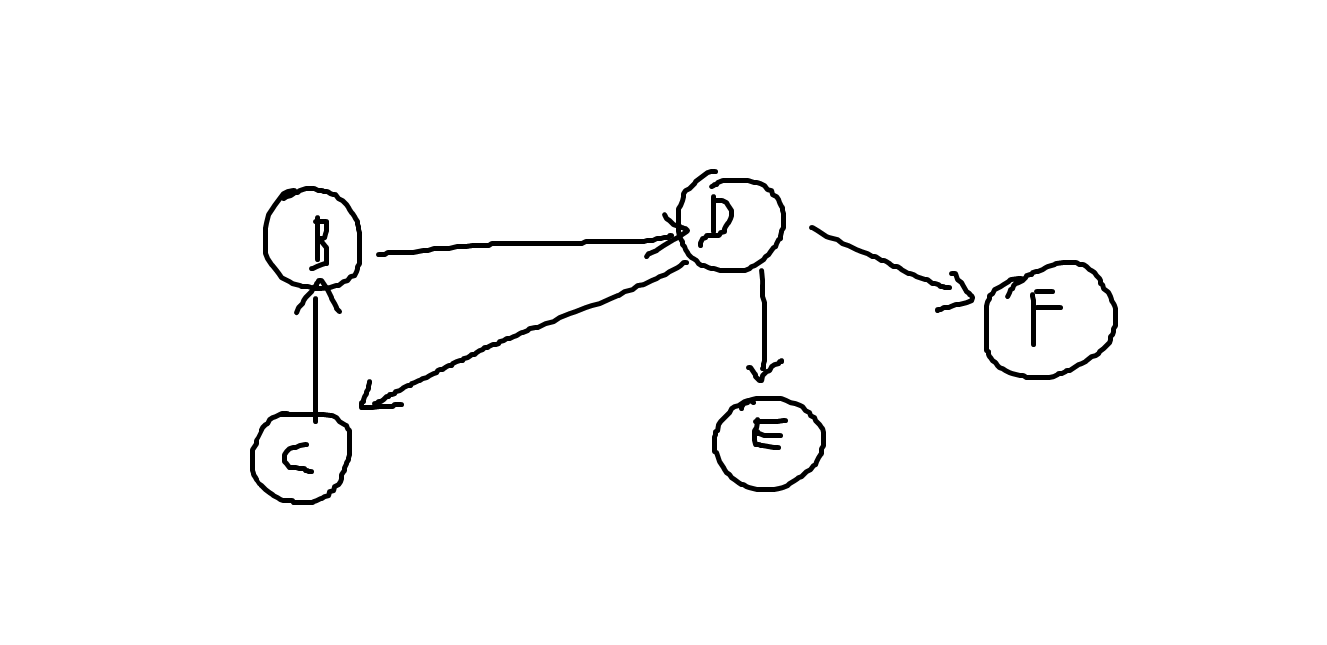
그런데 여기서 문제가 발생한다.
위상정렬은 진입차수가 0이 되는 노드를 지속해서 큐에 추가하면서 진행되는 알고리즘인데,
사이클로 인해서 (C에서 B로 들어가는 진입차수가 존재하기에 A에서 B로 가는 간선이 삭제되더라도 그 어느 노드도 진입차수가 0이 되지 않는다.) 이후로의 진행이 불가능함을 확인할 수 있다.
따라서
모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있습니다.
-> 사이클에 포함된 원소 중에서 어떠한 원소도 큐에 들어가지 못합니다.
에서 말한 것 처럼 사이클에 포함된 그 어느 원소도 큐에 들어가지 못하게 된다.
(그림으로 그리고 보니... 굳이 그림까지 그려야됬나 싶을 정도로 간단하게 확인이 되었다... ㄷㄷ )
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| Recursion in programming - youtube 영상 (0) | 2021.08.14 |
|---|---|
| Java vs Python3 vs C++ for coding test (0) | 2021.07.30 |
| RadixSort(기수정렬) 에서는 왜 낮은 자리수부터 비교해야 하는걸까 (0) | 2021.07.10 |
| 알고리즘 TIP1 (0) | 2021.06.25 |
| 알고리즘 스터디 (0) | 2021.06.23 |