제목과 동일한 질문을 교수님께 여쭤본 적이 있다.
답변은 아주 간단했는데, " MSD부터 정렬하게 되면 정렬이 되지 않습니다. " 였다.
사실 직접 해봤어야 했는데, 그 간단한 과정을 해보지 않고 질문을 해서 지금 생각해보니 조금 멍청한 질문이 아니었나 생각이 든다.
질문할 당시에는 왜 굳이 낮은 자리수부터 비교해야하는가에 대해 생각해보면서 낮은 자리수부터 비교한다면
A, B가 있다고 가정할때 A의 MSD가 B의 MSD보다 큼에도 불구하고 낮은 자리수부터 비교하면서 자리수를 거슬러 올라가는 과정에서는 그 사실을 알지 못함으로 A가 B보다 큼에도 계속해서 낮은 자리수를 비교함으로써 그것이 낭비라고 생각했다. 반면에 MSD부터 비교한다면 처음 비교할때부터 이미 A가 B보다 큼이 기정사실이 되어버리니 그 밑의 자리수는 비교할 필요가 없지 않을까라는 생각을 하게 되었기 때문이다.
그 당시에는 위 추측이 나름 합리적이고 허점을 짚어냈다고 생각했다. 물론 그림으로 한번만 풀어봤다면 틀렸다는걸 알았을텐데 말이다.
교수님의 답변을 듣고 나서 교수님의 말씀이 왜 맞는지에 대한지 깊게 생각해보지 않았고 내 질문이 실패로 돌아갔다는 아쉬움에 고개만 끄덕이고 지나갔다.
그래서 시간이 꽤 지났지만, 문득 떠올라서 직접 해보기로 했다. 정말 교수님 말대로 높은 자리수부터 정렬을 하게 되면 정렬이 안되는건가?
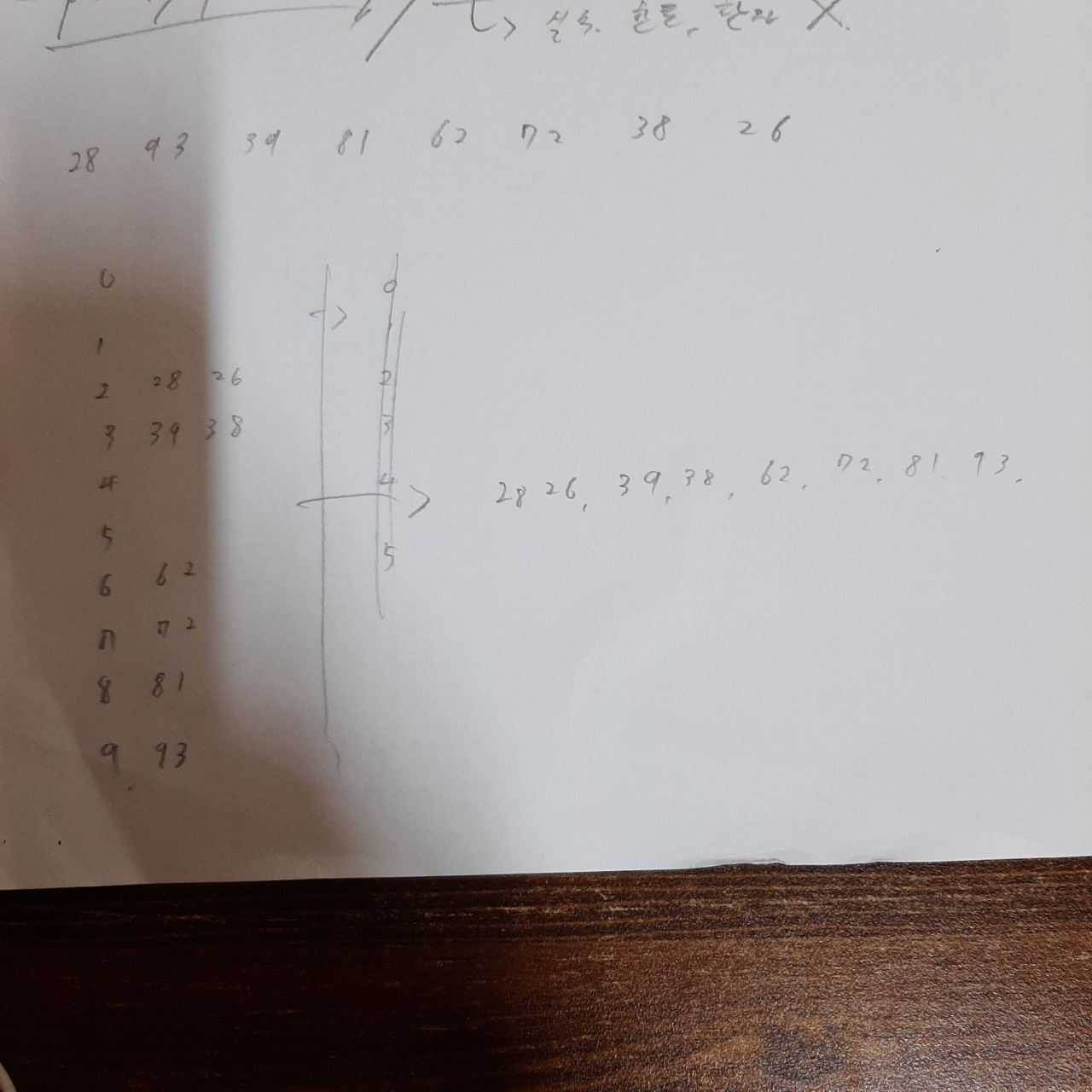
복잡한 과정이 필요했던 것도 아니고 끄적이자마자 바로 답이 나왔다. (실제로 정렬이 안된다. 해보면 진짜 안된다.)
교수님 말대로 높은 자리수부터 비교를 하게 되면 정렬이 되지 않는다. 좀 더 정확히 말하자면, 정렬이 완전 뒤죽박죽으로 안되는 것은 아니고, 정확한 정렬이 되지 않는다. 즉 높은 자리수(MSD)가 같은 숫자인 A,B,C,D... 가 있다고 가정하면
이 숫자들간에도 순서가 존재할텐데 바로 그 순서가 정렬되지 않는다.
따라서 이제와서 생각해보니 낮은 자리수부터 비교해가면서 버켓에 넣게되는 그 과정은 나중에 MSD를 비교하면서 최종적으로 결과를 산출해낼적에 같은 MSD를 갖고 있는 숫자들간에 정렬을 이뤄내게 하기 위함이라는 것을 알게 되었다.
위에 첨부된 사진에 필기가 있는데 필기에 너무 막 써놓았는데 나름 설명을 해보겠다.
28 93 39 81 62 72 38 26 이라는 숫자를 가지고 높은 자리수부터 버켓에 넣어본 것이다.
왼쪽에 0~9까지 세로로 숫자가 있는데, 그것들이 버켓이다.
그리고 그 버켓에서 순서대로 최종정렬을 진행하면, 28 26 39 38 62 72 81 93을 얻는다.
즉 28 26 을 보더라도 정렬이 진행되지 않았다. (완벽히 되지 않는다. 어설프게 되는거다.)
따라서 결론은 교수님의 말이 맞았고 다음부터 이런 류의 궁금점이 생기면 일단 먼저 내가 직접 계산해봐야겠다라는 생각이 든다. 그당시에 질문할 적에 한번만 써봤으면 바로 결론이 나왔을거라는 생각이 든다. 이해안되면 일단 종이꺼내서 끄적이면 된다. 난 머리가 그다지 좋지 않아서 머릿속에서 숫자들을 옮기고 적어놓고 하는게 안된다. 그러니 종이쓰자.
그런데 여기서 한가지 의문이 든다.
삽입정렬은 어느정도 정렬이 되어있다면 아주 빠르다는 장점이 존재한다. 그리고 그 점때문에 쉘정렬이 탄생하기도 했다. 그렇다면 지금 위에서 MSD부터 비교를 해서 나온 결과인 (아직 정렬이 덜됬지만 어느 정도 정렬이 된 결과물) 그 결과에
삽입정렬을 실행한다면 꽤 쓸만한 성능이 나올까? 결과가 어떻게 될지 궁금하다.
즉 MSD부터 비교하는 기수정렬 (음... 이러면 기수정렬이 아니긴한데 아무튼...) 을 실행한 후에 어느 정도 정렬이 진행되었으니 삽입정렬을 실행하면 아주 빠르게 정렬할 수 있지 않을까? (기수정렬이 실용성이 낮지만 그래도 준비된 조건하에 속도만 따져본다면 어째 가능할것 같기도 하다.)
비교대상은 아마 오리지널 삽입정렬 그 자체, 오리지널 기수정렬이 될 수 있을 것 같다.
아니면 쉘 정렬과도 비교해보면 재밌을 것 같다. (쉘 정렬하고 비교하는 게 맞는 것 같다.)
시험이 끝나면 직접 결과를 비교해보면 재밌을 것 같다.
결론:
"Radix Sort 에서는 높은 자리수부터 정렬하면 정렬이 되지 않는다. 따라서 낮은 자리수부터 정렬해야하는 것이 맞다. 그리고 질문하기 전에 먼저 계산해봅시다."
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| 위상 정렬 (Topological Sort)의 사이클 존재 판별 (0) | 2021.08.07 |
|---|---|
| Java vs Python3 vs C++ for coding test (0) | 2021.07.30 |
| 알고리즘 TIP1 (0) | 2021.06.25 |
| 알고리즘 스터디 (0) | 2021.06.23 |
| 알고리즘 설명해주는 블로그 (0) | 2020.12.24 |